Astrophotography camera for deep-sky: what to choose
Choosing from various astrophotography cameras for deep-sky imaging may seem complicated. In this article, through a series of practical examples, we will explore how to choose an astrophotography camera to capture even the faintest details of galaxies, nebulae, and star clusters with long exposures (these cameras differ from those used for planetary and lunar photography, which record short videos). Deep-sky astrophotography cameras are usually cooled, meaning they have a system with Peltier cells that cool and stabilize the sensor at low temperatures to reduce image noise and therefore improve quality.
In this article, we will encounter some technical terms that must be considered when choosing an astrophotography camera for deep-sky imaging:
– Resolution Capability: This is the minimum distance in arc seconds at which two objects can be identified as separate and is closely related to the telescope diameter. It is calculated with the formula a= 120 / D where “a” is the resolution capability in arc seconds, “120” is a constant, and “D” is the telescope diameter in millimeters.
– Seeing: This refers to the set of phenomena that contribute to the deterioration of image quality in both visual and photographic applications, such as atmospheric turbulence, humidity, and light pollution.
– Sampling: This is the most difficult concept to understand but is essential for choosing the right camera based on the telescope. It indicates how many arc seconds a single pixel of the sensor can record.
After this introduction, you may understand that if you already have a telescope, the choice of an astrophotography camera also depends on the sensor pixel size.

Sampling
Let’s start with a practical example using the Takahashi FSQ-85, which has a 85mm diameter and a 450mm focal length. Its resolution capability is calculated with the formula a=120/D, resulting in ( 120 / 85 = 1.41 ) arc seconds. According to the Nyquist principle, the pixel size of the sensor must cover more than half of the smallest detail that our telescope can resolve. Therefore, the astrophotography camera pixels must record the signal of an area of the sky equal to (1.41/2 = 0.70) arc seconds.
Starting with the formula
C = (206265 x d) / L
where:
• ( L ) = telescope focal length in millimeters
• ( d ) = sensor pixel dimensions in millimeters
• C = sampling value in arc seconds
• 206265 = conversion factor from radians to arc seconds
We can now calculate what we need to know to choose an astrophotography camera. We start with the analysis of a camera with Sony IMX571 sensor that, according to the technical specifications, comes with 3.76 microns pixels. Using the formula, we get a sample of:
(206265 x 0.00376) / 450 = 1.72 arc
This result is quite far from the theoretical value we calculated, indicating that we are undersampling the image. This means our camera is not capable of recording all the details that the optics can resolve. So, what do we do?
We must consider the seeing conditions, which include the effects of atmospheric turbulence responsible for the distortion of light passing through the Earth’s atmosphere before reaching our instrument. In areas with average seeing, seeing allows us to record finer details on 3-4 pixels. Therefore, applying the Nyquist principle, our sampling should be around 1.5 to 2 arc seconds. Often, it is unnecessary to go below these values, as we would upsample the image, meaning the maximum detail would be reported by more than two pixels. So the 1.72 arc seconds value obtained with the Sony IMX571 sensor is perfectly within the range dictated by seeing conditions, making it a good match for the Takahashi FSQ-85.
Do we want to search for the best sensor that will match our telescope? If we use the formula as a constant, setting the min and max value of our ideal sampling, we can calculate the min and max value of the pixel size of our hypothetical sensor, on the basis of theoretical sampling values from 1.5 to 2 arc seconds:
d = (L x C) / 206265
1) with 1,5 arc seconds: (450 x 1,5) / 206265 = 3,3 micron
2) with 2,0 arc seconds: (450 x 2) / 206265 = 4,4 micron
This means we can search for a sensor that comes with a pixel size dimension between 3,3 and 4,4 microns.
Other features: Type and Sensor Size
By having calculated the ideal size of the sensor pixels, we can now select an astrophotography camera based on other parameters, including:
– Sensor Type: Sensors for deep-sky astrophotography cameras may be color or monochrome. Color sensors allow you to get a color image directly and are easier to use than monochrome ones, which require a series of filters (such as an LRGB set) to reconstruct the image in color using special processing techniques. Monochrome cameras, however, have a significant advantage: they are more sensitive than their corresponding color sensors. This allows us to record weaker details with the same exposure time or record the same stellar magnitudes with a shorter exposure time than a color camera would require. More importantly, monochrome cameras allow the use of narrow-band filters against light pollution (such as H-alpha, OIII, and SII filters), which significantly increase nebula contrast against the sky background and allow astrophotography from areas with substantial light pollution.

So, the choice of sensor type also depends on the location from which you want to conduct astrophotography. If you have access to a site with little light pollution, you can choose a color astrophotography camera (perhaps using a broadband nebula filter to slightly reduce light pollution – in this case, the filter should not be too narrow to let more light pass through and avoid altered colors). If you are taking pictures from a place with evident light pollution, choose a monochrome camera. Monochrome cameras are almost always chosen by expert astrophotographers due to their added sensitivity, although they are more complex to use.
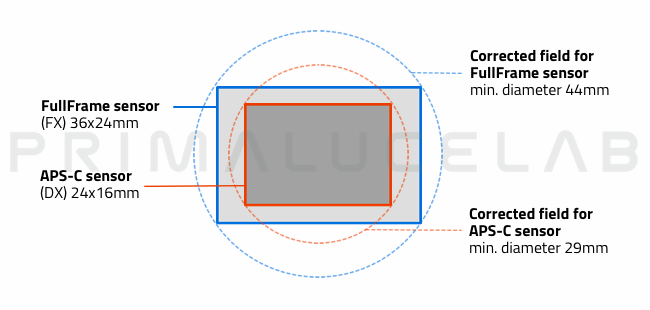
– Sensor Dimension: With the same telescope focal length, a larger sensor allows you to frame a greater area and is therefore preferred. However, astrophotography cameras with larger sensors are also more expensive, which is a factor to consider when choosing a camera for deep-sky imaging.
We must also consider the corrected area provided by the telescope. For example, it is pointless to buy a Full Frame sensor with a 43mm diagonal and then use it with a telescope that provides a corrected area of only 20mm (indicating the diameter of the corrected image circle generated by the telescope in which the stars are point-like). The result would be an image with elongated stars towards the edges. In our example with the Takahashi FSQ-85 provides a 44mm corrected field so we can choose also a very large Full Frame sensor.